Момент силы — Википедия
Момент силы, приложенный к гаечному ключу. Направлен от зрителя

Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы и вектора этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы (в предположении, что ось вращения проходит через начало координат).
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.
Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.
Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.
Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.
Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=π2−α{\displaystyle \beta ={\frac {\pi }{2}}-\alpha }, а так как cos(π2−α)=sinα{\displaystyle \cos {\left({\frac {\pi }{2}}-\alpha \right)}=\sin \alpha }, получаем, что |F→|cosβ=|F→|sinα{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.
Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sinα{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.
Теперь видно, что произведение |r→||F→|sinα{\displaystyle \left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin \alpha } есть не что иное, как модуль векторного произведения векторов r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}, то есть |r→×F→|{\displaystyle \left|{\vec {r}}\times {\vec {F}}\right|}, которое и было принято обозначить за момент силы M{\displaystyle M}, или модуль вектора момента силы |M→|{\displaystyle \left|{\vec {M}}\right|}.
Теперь полная работа записывается просто: A=∫0φ|r→×F→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {r}}\times {\vec {F}}\right|d\varphi }, или A=∫0φ|M→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {M}}\right|d\varphi }.
Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Энергия и механическая работа также имеют размерность «сила, умноженная на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина псевдовекторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля. Математически:
- E=Mθ,{\displaystyle E=M\theta ,}
где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.
Формула момента рычага[править | править код]
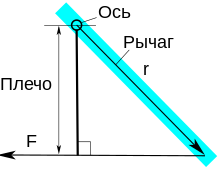 Момент, действующий на рычаг
Момент, действующий на рычагОчень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом[править | править код]
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие[править | править код]
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.
Момент силы как функция от времени[править | править код]
Момент силы — производная по времени от момента импульса,
Видеоурок: вращающий момент- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
- Mc→=Icdω→dt+[w→,Icw→].{\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+[{\vec {w}},I_{c}{\vec {w}}].}
Отношение между моментом силы и мощностью[править | править код]
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Так же и момент силы, если совершает действие через угловое расстояние, он совершает работу.
- P=M→⋅ω→.{\displaystyle P={\vec {M}}\cdot {\vec {\omega }}.}
В системе СИ мощность P{\displaystyle P} измеряется в ваттах, момент силы — в ньютоно-метрах, а угловая скорость — в радианах в секунду.
Отношение между моментом силы и работой[править | править код]
- A=∫θ1θ2|M→|dθ.{\displaystyle A=\int _{\theta _{1}}^{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}
В случае постоянного момента получаем:
- A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}
В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютоно-метрах, а угол — в радианах.
Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}.
Тогда совершённая моментом силы работа рассчитывается как:
- A=|M→|ωt.{\displaystyle A=\left|{\vec {M}}\right|\omega t.}
Если имеется материальная точка OF{\displaystyle O_{F}}, к которой приложена сила F→{\displaystyle {\vec {F}}}, то момент силы относительно точки O{\displaystyle O} равен векторному произведению радиус-вектора r→{\displaystyle {\vec {r}}}, соединяющего точки O{\displaystyle O} и OF{\displaystyle O_{F}}, на вектор силы F→{\displaystyle {\vec {F}}}:
- MO→=[r→×F→].{\displaystyle {\vec {M_{O}}}=\left[{\vec {r}}\times {\vec {F}}\right].}
Момент силы относительно оси равен алгебраическому значению проекции момента этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть
- Mz(F)=Mo(F′)=F′h′.{\displaystyle M_{z}(F)=M_{o}(F’)=F’h’.}
Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными, индуктивными, ультразвуковыми, механическими.
Существуют специальные динамометрические ключи для измерения крутящего момента затягивания резьбовых соединений и регулируемые и нерегулируемые ограничители крутящего момента, так называемые «трещотки», применяемые в гаечных ключах, шуруповёртах, винтовых микрометрах и др.
Мощность или на крутящий момент? — Рамблер/авто
Когда речь заходит о выборе машины, то большинство людей смотрит на максимальную мощность. Они считают, что это важнейшая характеристика двигателя. Меньше людей смотрит на крутящий момент, считая, что именно он правит балом. Кое-кто смотрит и на мощность, и на крутящий момент, но цифры в технических характеристиках всё равно почти ничего не значат в реальной жизни. Гораздо важнее обороты двигателя, на которых достигаются пиковые значения. Но и это ещё не всё, и вот почему.
Чего хочет водитель
Цифры можно сравнивать, но большее значение мощности или крутящего момента не говорит о том, что в реальной жизни машина при прочих равных будет быстрее, а двигатель, как говорят, эластичнее. Смотреть нужно на графики. Графики крутящего момента и мощности в зависимости от оборотов двигателя одновременно. Чем больше крутящий момент на низах, чем ближе крутящий момент к максимальному на средних оборотах и чем позже достигается максимальная мощность, тем лучше. По сути, это и есть формула идеального мотора, но достигнуть её очень тяжело.
Генри Форд в свое время говорил: «Мощность продает автомобиль, но гонки выигрывает крутящий момент».Ещё он говорил: «Спросите любого водителя, чего он хочет, и он ответит, что хочет больше мощности».
Обе цитаты в полной мере верны и сегодня, но вернемся к теме. Нельзя рассуждать о мощности и крутящем моменте по-отдельности по одной простой причине — и тут, возможно, для кого-то сейчас я открою Америку: мощность и крутящий момент связаны между собой. В упрощенном виде зависимость выглядит так (не пугайтесь, это единственная формула в этой статье): N=k*M*n, где N — это мощность, k-это постоянный коэффициент для перевода в нужные физические величины (Вт, кВт, л.с.), а n — это обороты двигателя (те, самые, которые указываются на тахометре).
Из этой формулы следует, что чем больше крутящий момент, тем больше мощность. Обращаю, кстати, внимание на то, что именно мощность зависит от крутящего момента, а не наоборот. Таким образом, так как у дизельных моторов большой крутящий момент, у них должна быть и высокая мощность, но на первый взгляд это не так.
Дизельный парадокс
Давайте для примера возьмем два мотора BMW: 3-литровый бензиновый и 3-литровый дизельный. У первого крутящий момент 400 Нм при 1200-5000 об/мин, а мощность 306 л.с. при 5800-6000 об/мин. У дизельного же крутящий момент больше — 560 Нм при 1500-3000 об/мин, но мощность меньше — 258 л.с. при 4000 об/мин. Почему так?Все дело в оборотах, при которых достигается максимальная мощность. Дизельный мотор в силу своей конструкции не может выдавать большие обороты, но теоретически, если бы его можно было раскрутить до бензиновых 6000 оборотов в минуту, его мощность составляла бы 479 л.с.
По этой же причине малообъемные, но высокооборотистые мотоциклетные и гоночные двигатели при небольшом крутящем моменте выдают огромные мощности. Но вернемся к реальной жизни. На что же смотреть при покупке автомобиля, раз крутящий момент и мощность взаимозависимы?
Турбомоторы рулят
Смотреть нужно на графики распределения мощности и крутящего момента по всему диапазону работы мотора. Так, сравнивая типичный атмосферник и турбомотор, можно сделать три вывода.
Чем раньше достигается максимальный крутящий момент, тем лучше. По этому параметру выигрывает турбированный мотор.
Чем позже достигается пик мощности, тем лучше. По этому параметру у моторов паритет.
Чем ближе к максимальному крутящий момент на средних оборотах. тем лучше. Тут снова выигрывает турбированный, потому что на средних оборотах у него как раз максимум.
Что ещё можно сказать? Ну, например, то, что у турбированного мотора будет ровная тяга в среднем диапазоне оборотов, а ближе к красной зоне будет резкий спад тяги. У атмосферного мотора тяга будет увеличиваться и уменьшаться равномерно.
Новости авто: Самые надежные моторы объемом 2+ литра
Обзор рынка: «АвтоВАЗ» рассекретил цены на спортивную Lada GrantaВидео дня. Дежурство с «Дорожным патрулем» ЦОДД
Читайте также
Крутящий момент, что это и зачем он нужен?
Каждый двигатель внутреннего сгорания рассчитан на определенную максимальную мощность, которую он может выдавать при наборе определенного количества оборотов коленчатого вала. Однако помимо максимальной мощности существует еще и такая величина в характеристике двигателя, как максимальный крутящий момент, достигаемый на оборотах отличных от оборотов максимальной мощности.
Что же означает понятие крутящий момент?
Говоря научным языком, крутящий момент равен произведению силы на плечо ее применения и измеряется в ньютон — метрах. Значит если к гаечному ключу длиной 1 метр (плечо), приложить силу в 1 Ньютон (перпендикулярно на конце ключа), то мы получим крутящий момент равный 1 Нм.
Для наглядности. Если гайка затянута с усилием 3 кгс, то для ее откручивания придется к ключу с длиной плеча в 1 метр приложить усилие 3 кг. Однако, если на ключ длиной 1 метр надеть дополнительно 2-х метровый отрезок трубы, увеличив тем самым рычаг до 3 метров, то тогда для отворачивания этой гайки потребуется лишь усилие в 1 кг. Так поступают многие автолюбители при откручивании колесных болтов: либо добавляют отрезок трубы, а за неимением такового просто надавливают на ключ ногой, увеличив тем самым силу приложения к баллонному ключу.
Так же если на рычаг метровой длины повесить груз равный 10 кг, то появится крутящий момент равный 10 кгм. В системе СИ это значение (перемножается на ускорение свободного падения — 9,81 м/см2) будет соответствовать 98,1 Нм.
Результат всегда един — крутящий момент, это произведение силы на длину рычага, стало быть, нужен либо длиннее рычаг, либо большее количество прикладываемой силы.
 Показатели ньютон-метров на примере двигателя V6 3,5 литра Lexus GS450h
Показатели ньютон-метров на примере двигателя V6 3,5 литра Lexus GS450hВсе это хорошо, но для чего нужен крутящий момент в автомобиле и как его величина влияет на его поведение на дороге?
Мощность двигателя лишь косвенно отражает тяговые возможности мотора, и ее максимальное значение проявляется, как правило, на максимальных оборотах двигателя. В реальной жизни в таких режимах практически никто не ездит, а вот ускорение двигателю требуется всегда и желательно с момента нажатия на педаль газа. На практике одни автомобили уже с низких оборотов (с низов) ведут себя достаточно резво, другие напротив предпочитают лишь высокие обороты, а на низах показывают вялую динамику.
Так у многих возникает масса вопросов, когда они с авто с бензиновым мотором мощностью 105-120 л.с. пересаживаются на 70-80 – сильный дизель, то последний с легкостью обходит машину с бензиновым мотором. Как такое может быть?
Связано это с величиной тяги на ведущих колесах, которая различна для этих двух автомобилей. Величина тяги напрямую зависит от произведения таких показателей как, величины крутящего момента, передаточного числа трансмиссии, ее КПД и радиуса качения колеса.
Как создается крутящий момент в двигателе
В двигателе нет метровых рычагов и грузов, и их заменяет кривошипно-шатунный механизм с поршнями. Крутящий момент в двигателе образуется за счет сгорания топливо — воздушной смеси, которая расширяясь в объеме с усилием толкает поршень вниз. Поршень в свою очередь через шатун передает давление на шейку коленчатого вала. В характеристике двигателя нет значения плеча, но есть величина хода поршня (двойное значение радиуса кривошипа коленвала).
Для любого мотора крутящий момент рассчитывается следующим образом. Когда поршень с усилием 200 кг двигает шатун на плечо 5 см, появляется крутящий момент 10 кГс или 98,1Нм. В данном случает для увеличения крутящего момента нужно либо увеличить радиус кривошипа, или же увеличить давление расширяющихся газов на поршень.
До определенной величины можно увеличить радиус кривошипа, но будут расти и размеры блока цилиндров как в ширину, так и в высоту и увеличивать радиус до бесконечности невозможно. Да и конструкцию двигателя придется значительно упрочнять, так как будут нарастать силы инерции и другие отрицательные факторы. Следовательно, у разработчиков моторов остался второй вариант – нарастить силу, с которой поршень передает усилие для прокручивания коленвала. Для этих целей в камере сгорания нужно сжечь больше горючей смеси и к тому же более качественно. Для этого меняют величину и конфигурацию камеры сгорания, делают «вытеснители» на головках поршней и повышают степень сжатия.
Однако максимальный момент доступен не на всех оборотах мотора и у различных двигателей пик момента достигается на различных режимах. Одни моторы выдают его в диапазоне 1800- 3000 об/мин, другие на 3000-4500 об/мин. Это зависит от конструкции впускного коллектора и фаз газораспределения, когда эффективное наполнение цилиндров рабочей смесью происходит при определенных оборотах.
Наиболее простое решение для увеличения крутящего момента, а следовательно и тяги, это применение турбо или механического наддува, либо применение их в комплексе. Тогда крутящий момент можно уже использовать с 800-1000 об/мин, т.е. практически сразу при нажатие на педаль акселератора. К тому же это закрывает такую проблему, как провалы при наборе скорости, так как величина КМ становится практически одинакова во всем диапазоне оборотов двигателя. Достигается это различными путями: увеличивают количество клапанов на цилиндр, делают управляемыми фазы газораспределения для оптимизации сгорания топлива, повышают степень сжатия, применяют выпускной коллектор по формуле 1-4 -2-3, в турбинах применяют крыльчатки с изменяемым и регулируемым углом атаки лопаток и т.д.
Что такое крутящий момент и почему его показатель важнее лошадиных сил? | Об автомобилях | Авто
Подавляющее большинство автопроизводителей в маркировке своих двигателей использует мощность или объем камер сгорания. Обе этих характеристики уже устарели. Если 50 лет назад тяга карбюраторных моторов зависела от расточки цилиндров, то сейчас на первый план выходят новые технологии. При одинаковом объеме камер сгорания мощность вырастает в два-три раза. К примеру, сейчас небольшие 2,0-литровые рядные моторы BMW или Volvo могут иметь мощность свыше 400 лс. Тем самым, бензиновые 4-цилиндровые турбированные моторы небольшого объема сейчас располагают такой же мощностью и тягой, как 8-цилиндровые атмосферники 15-летней давности, потому как оснащены помимо ступенчатого наддува еще и сложной системой впрыска.
Но и лошадиные силы уже недостаточно адекватно описывают существующие характеристики двигателя. Автомобиль с небольшой мощностью может казаться значительно резвее и интереснее на дороге, чем другой более мощный собрат. К примеру, дизельные агрегаты намного опережают бензиновые по тяге, а значит, показывают лучшую динамику.
В общем, потребовалась иная характеристика, которая бы могла адекватно описывать возможности современного мотора. И автопроизводители видят ее в крутящем моменте.
Откуда берутся «лошадиные силы»?
Измерять мощность моторов в «лошадиных силах» предложил знаменитый английский изобретатель Джеймс Уатт в 1789 году. Во времена начала промышленной революции в Англии на рудниках, в портах и мельницах в качестве источника силы для подъемных машин использовались лошади. Их запрягали в лебедку крана и гоняли по кругу.
Запряженное в механизм животное весом около 500 кг, вышагивая по кругу и натягивая канат через систему блоков, могло обеспечить работу крана, равную подъему груза в 90 кг со скоростью 1 метр в секунду. Груз поднимали бочками или кулями весом от 140,9 до 190,9 кг каждый. Тем самым, за 8 часов работы лошадь, ковыляя вокруг лебедки со скоростью в 3 км\ч, не утруждаясь могла перегрузить 33 000 фунтов, что равняется почти 14 тоннам. Эту работу и прописали как эталон «лошадиной силы».
Паровые машины могли совершать такую же работу гораздо быстрее, потому как имели мощность в несколько лошадиных сил. Тем самым, в определении Джеймса Уатта, мощность — это не спортивная динамика машины, не приемистость, а работа, совершенная в единицу времени.
А что же такое крутящий момент?
В двигателе внутреннего сгорания применяется тот же принцип. Только силой, толкающей поршень, является энергия взрывов смеси бензина и воздуха. Поршень аналогичен той самой уаттовской лошади. Он раскручивает коленвал, а дальше через систему валов трансмиссии передает движение на колеса. Чем быстрее он вращается, тем выше мощность и больше работы выполнит мотор.
Если силу давления поршней умножить на длину рычага кривошипа, то получим крутящий момент, от которого зависит тяга мотора. Она выражается в Ньютонметрах (1 Нм равен силе в 1 ньютон, умноженной на рычаг в 1 метр). Чем длиннее рычаги, тем больше тяги выдает мотор.
Если у мотора высокий крутящий момент, то колеса за единицу времени раскручиваются быстрее. Автомобиль приобретает больше динамики.
Ураганный разгон
Итак, крутящий момент это очень важная характеристика, от которой зависит динамика машины. Чем выше крутящий момент, тем «лошади» под капотом становятся сильнее. С помощью крутящего момента определяется так же эластичность мотора, то есть его способность обеспечивать одинаковую тягу в большом диапазоне оборотов. В особенности важно, чтобы высокий крутящий момент был доступен почти сразу после старта. Тогда будет ощущаться эмоциональное ускорение автомобиля.
Ну а лошадиные силы нужны для другого. Они выражают способность мотора автомобиля сопротивляться ветровым и прочим нагрузкам. Высокая мощность отражается в основном на максимальной скорости машины.
Вообще, «лошадиные силы» очень ненадежная характеристика, зависимая от множества факторов. Эта единица измерений давно устарела. С помощью хитрых программ управления двигателем количество «лошадиных сил» можно прибавить или уменьшить, чем и пользуются многие производители, искусственно раздувающие мощность мотора.
Поэтому количество Нм крутящего момента в маркировке моторов гораздо более информативная характеристика.
Крутящий момент — это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
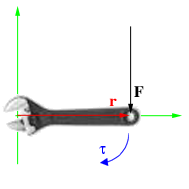
Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
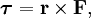
где  — сила, действующая на частицу, а
— сила, действующая на частицу, а 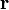 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы  на рычаг
на рычаг  , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 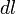 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 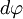 . Обозначим через
. Обозначим через 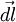 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 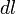 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы  и вектором
и вектором 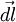 равен
равен 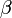 , а угол
, а угол 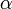
 и вектором силы
и вектором силы  .
.
Следовательно, бесконечно малая работа 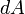 , совершаемая силой
, совершаемая силой  на бесконечно малом участке
на бесконечно малом участке 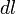 равна скалярному произведению вектора
равна скалярному произведению вектора 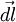 и вектора силы, то есть
и вектора силы, то есть 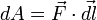 .
.
Теперь попытаемся выразить модуль вектора 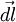 через радиус вектор
через радиус вектор  , а проекцию вектора силы
, а проекцию вектора силы  на вектор
на вектор 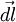 , через угол
, через угол 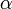 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 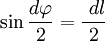 , где в случае малого угла справедливо
, где в случае малого угла справедливо 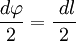 и следовательно
и следовательно 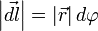
Для проекции вектора силы  на вектор
на вектор 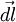 , видно, что угол
, видно, что угол  , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 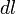 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу  , а так как
, а так как 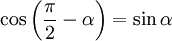 , получаем, что
, получаем, что 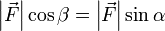 .
.
Теперь запишем бесконечно малую работу через новые равенства 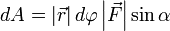 или
или 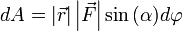 .
.
Теперь видно, что произведение 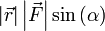 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов  и
и  , то есть
, то есть 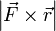 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 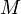 или модуля вектора момента силы
или модуля вектора момента силы 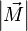 .
.
И теперь полная работа записывается очень просто 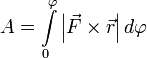 или
или 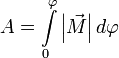 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
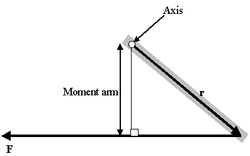
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 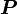 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 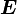 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 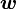 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 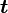 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 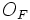 , к которой приложена сила
, к которой приложена сила  , то момент силы относительно точки
, то момент силы относительно точки 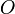 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора  , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы  :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/biograf.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Крутящий момент — это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
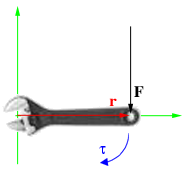
Момент силы приложенный к гаечному ключу
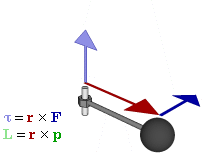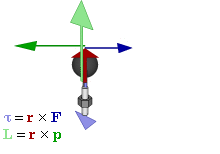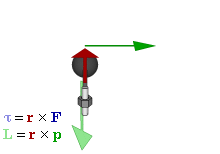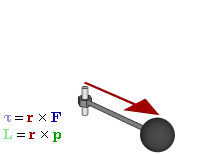
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
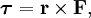
где 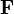 — сила, действующая на частицу, а
— сила, действующая на частицу, а 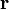 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 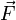 на рычаг
на рычаг 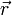 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 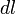 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 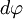 . Обозначим через
. Обозначим через 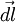 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 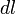 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 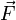 и вектором
и вектором 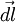 равен
равен 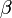 , а угол
, а угол 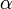
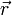 и вектором силы
и вектором силы 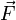 .
.
Следовательно, бесконечно малая работа 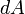 , совершаемая силой
, совершаемая силой 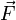 на бесконечно малом участке
на бесконечно малом участке 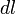 равна скалярному произведению вектора
равна скалярному произведению вектора 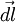 и вектора силы, то есть
и вектора силы, то есть 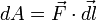 .
.
Теперь попытаемся выразить модуль вектора 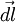 через радиус вектор
через радиус вектор 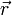 , а проекцию вектора силы
, а проекцию вектора силы 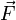 на вектор
на вектор 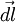 , через угол
, через угол 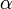 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 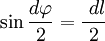 , где в случае малого угла справедливо
, где в случае малого угла справедливо 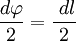 и следовательно
и следовательно 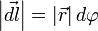
Для проекции вектора силы 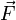 на вектор
на вектор 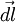 , видно, что угол
, видно, что угол 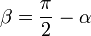 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 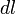 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 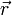 , а так как
, а так как 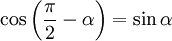 , получаем, что
, получаем, что 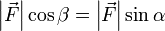 .
.
Теперь запишем бесконечно малую работу через новые равенства 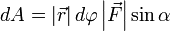 или
или 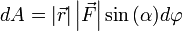 .
.
Теперь видно, что произведение 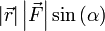 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 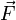 и
и 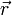 , то есть
, то есть 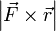 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 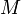 или модуля вектора момента силы
или модуля вектора момента силы 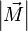 .
.
И теперь полная работа записывается очень просто 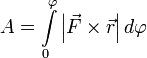 или
или 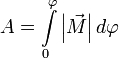 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
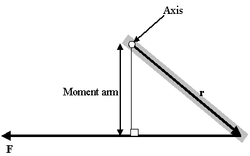
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность  измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 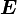 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 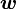 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 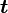 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 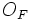 , к которой приложена сила
, к которой приложена сила 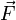 , то момент силы относительно точки
, то момент силы относительно точки  равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 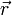 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 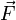 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/dic.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Крутящий момент — это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
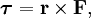
где  — сила, действующая на частицу, а
— сила, действующая на частицу, а 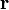 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы  на рычаг
на рычаг  , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 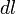 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 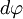 . Обозначим через
. Обозначим через 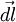 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 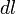 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы  и вектором
и вектором 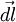 равен
равен 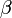 , а угол
, а угол 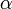
 и вектором силы
и вектором силы  .
.
Следовательно, бесконечно малая работа 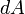 , совершаемая силой
, совершаемая силой  на бесконечно малом участке
на бесконечно малом участке 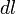 равна скалярному произведению вектора
равна скалярному произведению вектора 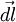 и вектора силы, то есть
и вектора силы, то есть 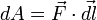 .
.
Теперь попытаемся выразить модуль вектора 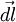 через радиус вектор
через радиус вектор  , а проекцию вектора силы
, а проекцию вектора силы  на вектор
на вектор 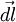 , через угол
, через угол 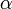 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 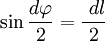 , где в случае малого угла справедливо
, где в случае малого угла справедливо 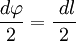 и следовательно
и следовательно 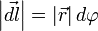
Для проекции вектора силы  на вектор
на вектор 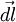 , видно, что угол
, видно, что угол  , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 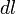 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу  , а так как
, а так как 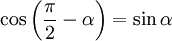 , получаем, что
, получаем, что 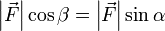 .
.
Теперь запишем бесконечно малую работу через новые равенства 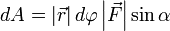 или
или 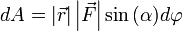 .
.
Теперь видно, что произведение 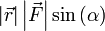 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов  и
и  , то есть
, то есть 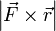 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 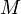 или модуля вектора момента силы
или модуля вектора момента силы 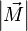 .
.
И теперь полная работа записывается очень просто 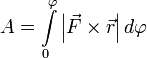 или
или 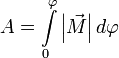 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага

Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 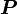 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 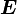 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 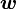 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 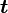 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 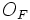 , к которой приложена сила
, к которой приложена сила  , то момент силы относительно точки
, то момент силы относительно точки 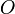 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора  , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы  :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/biograf.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
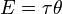 ,
, = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ ,
,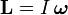 ,
,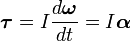 ,
,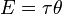 ,
,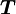 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ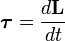 ,
,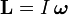 ,
,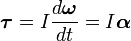 ,
,