ИНЕРЦИЯ И МОМЕНТ ИНЕРЦИИ: базовые сведения » РобоВики
В этой статье
- История понятия «инерция»
- Инерция, кинетическая энергия, работа
- Момент инерции
- Вопросы
До эпохи Возрождения, в Средние века, в западной философии общепринятой была аристотелевская теория движения. Ученик Платона, древнегреческий философ Аристотель (384 – 322 гг. до н. э.) утверждал, что в отсутствии внешней силы все объекты остановятся, и что движущиеся объекты продолжают двигаться только до тех пор, пока есть побуждающая к движению сила.
Бюст Аристотеля. Римская копия греческого бронзового оригиналаЭто утверждение закономерно вытекало из реальных наблюдений. При этом Аристотель объяснял движение снарядов, выпущенных из орудия, невидимым действием окружающей среды, которая каким-то образом продолжает двигать снаряд. При этом философ пришел к выводу, что такое движение в пустоте невозможно.
Принцип движения по инерции, который возник у Аристотеля для «движений в пустоте», гласил, что объект имеет тенденцию сопротивляться изменению движения.
Эта теория движения неоднократно оспаривалась. Например, в 6 веке византийский филолог Иоанн Александрийский (Иоанн Грамматик) раскритиковал тезисы Аристотеля, что среда поддерживает движения тела и что тело остановится в пустоте. В 11 веке персидский исламский врач, астроном, философ и писатель Ибн Сина [Авиценна] (980 – 1037 гг.) сделал вывод, что снаряд при отсутствии действия внешних сил, то есть в пустоте, не остановится.
Окончательно от аристотелевской теории отказались в ходе ряда открытий, предшествовавших научной революции XVII века.
Портрет Кеплера в 1610 годуТермин «инерция», от латинского слова «безделье» или «лень» (лат. inertia), был впервые использован немецким математиком и астрономом Иоганном Кеплером (1571 – 1630 гг.) в его книге «Epitome Astronomiae Copernicanae», которая была опубликована в трех частях в 1617–1621 гг. Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.
Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.
Покой и движение объединил единым принципом современник Кеплера Галилео Галилей (1564 — 1642) — итальянский физик, механик, астроном, философ и математик. Он первый, кто направил зрительную трубу в небо, превратив её в телескоп. В 1609 году он создал свой первый телескоп с трёхкратным увеличением. Галилео Галилей писал, что «если устранить все внешние препятствия, то тяжелое тело на сферической поверхности, концентрической Земле, будет поддерживать себя в том состоянии, в котором оно находилось; если его поместить в движение к западу (например), то оно будет поддерживать себя в этом движении».
Чтобы оспорить идею Аристотеля о естественности состояния покоя, Галилей проводил один из таких мысленных экспериментов.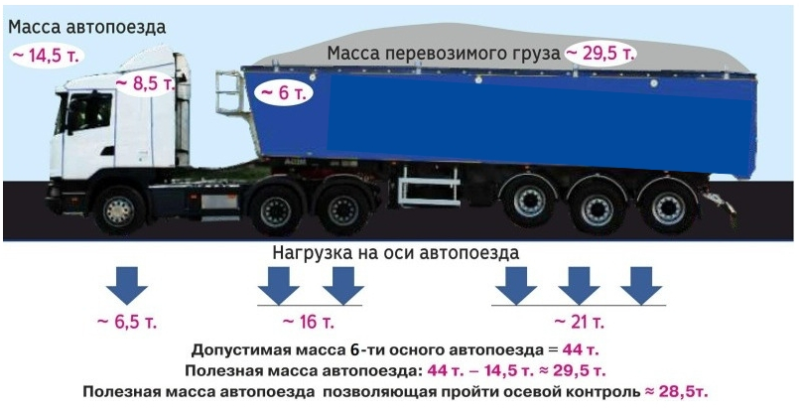 Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.
Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.
Галилей сделал вывод, что «Тело, движущееся по ровной поверхности, будет продолжать движение в том же направлении с постоянной скоростью, если движение не будет нарушено».
Готфрид Кнеллер. Портрет Исаака Ньютона. 1689Позднее, мысли Галилея будут уточнены и систематизированы Исааком Ньютоном. Исаак Ньютон (1642 – 1727) — английский физик, математик, механик и астроном, основатель классической физики. В своем труде «Математические начала натуральной философии» (Philosophiae Naturalis Principia Mathematica), впервые опубликованном в 1687 году, он изложил закон всемирного тяготения и три закона динамики.
Явление инерции, изначально сформулированное Галилеем, вошло в первый закон Ньютона.
Оговоримся, что согласно определению, законы Ньютона справедливы только для систем отсчета (система отсчета – это тело отсчета со связанной с ним системой координат, относительно которого можно вычислять положение тел, и система измерения времени, т.е. некоторые часы), которые принято называть инерциальными. Инерциальная система отсчета – это такая система, в которой ускорение тел зависит только от приложенных сил, а не свойством самой системы отсчета (наблюдателя) перемещаться с ускорением.
Посмотрим на второй закон Ньютона.
Чаще его записывают в виде:
так как в инерциальной системе отсчета сила является причиной ускорения тела.
Как видно из второй формулы, для тела неизменной массы ускорение тела (скорость изменения его скорости) прямо пропорционально силе, приложенной к телу (чем сильнее толкаем, тем быстрее тело разгоняется) и обратно пропорционально его массе (чем тяжелее тело, тем сложнее его разгонять).
Представим, что тело движется в вакууме и на него не действуют никакие силы (F=0). Значит и скорость его меняться не будет (a=0).
Инерция (лат. inertia — покой, постоянство, неизменность) – природное явление сохранения равномерного прямолинейного движения или состояния покоя любого тела, пока на него не действуют внешние силы или если действие сил скомпенсировано.
Инертность – свойство конкретного тела оставаться в покое или равномерно прямолинейно двигаться. От инертности зависит ускорение тела при приложении к нему внешних сил. Мерой количественного измерения инертности тела в прямолинейном движении является его масса. Больше масса – больше инертность тела, т.е. тем сложнее придать ему ускорение (разогнать или остановить).
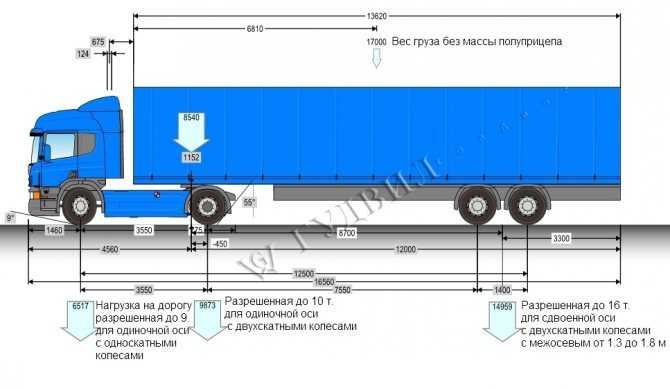
Тормозной путь грузовика и легковушкиИз-за большей чем у легковушки массы у грузовика инертность выше. Соответственно, и тормозной путь у него будет больше – нужно приложить большую силу, чтоб его остановить (хотя, можно поставить очень мощные тормоза). Говорить, что у грузовика больше инерция – некорректно.
Говорить, что у грузовика больше инерция – некорректно.
Мерой инертности тела в прямолинейном движении выступает его масса. Больше масса – больше инертность тела.
Инерция, кинетическая энергия, работа
Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.
Силачи тянут Ил-76А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.
Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.
Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):
Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).
Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.
Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:
Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.
Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.
При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?
Момент инерцииИнерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.
Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.
Ну а со спинерами и волчками знакомы многие.
Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?
Вращение на фигурном катанииМногие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.
Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:
Скорость вращающегося телаПри этом кинетическая энергия вращающегося тела примет вид:
Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).
Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).
Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.
Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:
Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.
Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.
Некоторые формулы для расчета момента инерции для тел разной формыПример.
Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r1 < r2), скатываются с горки высотой h. Какой цилиндр скатится быстрее? Какое из тел обладает меньшей инертностью?
Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой hВ верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.
Потенциальная и кинетическая энергия 1 и 2 цилиндра верхней точкеПри скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.
Кинетическая энергия первого и второго цилиндра в нижней точкеНо так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:
Тогда для кинетической энергии поступательного движения будет справедливо отношение:
Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.
Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.
Вопросы
1. Посмотри на картинку с формулами для расчета момента инерции для тел разной формы. Как ты думаешь, какая формула лучше подходит для расчёта момента инерции маховика автомобиля. Варианты ответа: a, b, c, d, e, f, g, h, или i
Маховик автомобиля2. Два волчка одинаковой массы раскрутили до одинаковой угловой скорости, но диаметр первого волчка меньше диаметра второго. Какой из них упадет раньше?
3. На рисунке показаны три варианта конструкции. Какой вариант машинки имеет наименьшую инертность, а какой максимальную? Почему?
Видео:
- Инерция. GetAClass
- Момент инерции. GetAClass
- Момент инерции вращающихся тел. Эксперимент. Зависимость момента инерции от распределения массы
- Момент инерции вращающихся тел.
 Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера
Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера - Момент инерции вращающихся тел. Фигурное катание. Юлия Липницкая, вращение
- Момент инерции. Работа двигателя с маховиком и без него
Статьи:
- Первый закон Ньютона и инерциальные системы отсчёта
- Второй закон Ньютона
- Равнодействующая
- Третий закон Ньютона
- Неинерциальные системы отсчёта
Большая часть энергии Физика Касьянов 10 класс 279 – Рамблер/класс
Большая часть энергии Физика Касьянов 10 класс 279 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Добрый день! Мне нужна Ваша помощь в задаче:
Какой молоток (лёгкий или тяжёлый) при ковке теряет большую часть своей энергии? Почему?
ответы
Воспользуемся формулой из учебника, которая определяет часть кинетической энергии грузовика, которая расходуется на деформацию грузовика:
где m1 – масса грузовика, m2 – масса легкового автомобиля. Применительно к нашему вопросу m1 – масса молотка, а m2 – масса наковальни — постоянная величина.
Применительно к нашему вопросу m1 – масса молотка, а m2 – масса наковальни — постоянная величина.
Перепишем выражение для γ так:
Теперь понятно, что если отношение будет меньше, то γ будет больше. Таким образом, тяжелый молоток при ковке теряет большую часть своей кинетической энергии, чем легкий молоток.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
ДосугХимия
похожие вопросы 5
Звуковые волны Физика Касьянов 10 класс 602
Добрый день! Укажите примерные размеры источников, генерирующих инфразвуковые, звуковые и ультразвуковые волны.
(Подробнее…)
ГДЗФизикаКасьянов В.А.10 класс
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
ГДЗ Тема 21 Физика 7-9 класс А. В.Перышкин Задание №476 Изобразите силы, действующие на тело.
В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Страница не найдена (404)
Страница не найдена (404)Такой страницы не существует!
Попробуйте выполнить одно из следующих действий:
- Если вы ввели адрес страницы в строку веб-адреса, убедитесь, что он написан правильно.

- Посетите домашнюю страницу pwc.com и найдите ссылки на информацию, которую вы хотеть.
- Или ознакомьтесь с нашей картой сайта.
Sidan du letar efter kan inte hittas!
Försök med något av följande:
- Kontrollera addressen och försök igen.
- Återvänd до foregående sida.
- Перейти на www.pwc.com/search leta после соответствующей информации.
- Письмо для карты сайта.
Эта страница не существует.
Попробуйте выполнить одно из следующих действий:
- Убедитесь, что вы правильно ввели URL-адрес
- Посетите домашнюю страницу PwC Canada
- Посетите нашу карту сайта
- или свяжитесь с нами
Ден сторона находит икке.
Fortvivl ej… prøv i stedet at:
- Перейти к pwc.dk forsiden
- Пройдено до вершины p5 pwc.
 dk
dk - Led i vores карта сайта
- Найти и др. PwC kontor i nærheden af dig
La page que vous demandez est introuvable.
Essayez l’une des Solutions suivantes :
- Assurez-vous que l’adresse URL-адрес страницы, которая является правильной
- Посетите страницу аккумулирования на сайте PwC Canada
- Посетите план сайта
- Оу, контактный номер
Diese Seite Exsiert nicht oder ist nicht mehr verfügbar. Bitte versuchen Sie Folgendes:
- Wenn Sie die Adresse manuell eingegeben haben, prüfen Sie diese auf Tippfehler.
- Besuchen Sie die Startseite und verwenden Sie diesuchfunktion.
Запрошенная вами страница не найдена. Если вы ищете информацию по определенной теме, пожалуйста, воспользуйтесь функцией поиска по сайту выше. В качестве альтернативы вот текущая карта сайта.
Если вы хотите поговорить с кем-нибудь из PwC о текущем бизнес-вопросе или получить дополнительную информацию о конкретной теме или о PwC и предоставляемых нами услугах, вы можете позвонить номер нашего главного коммутатора: +44 (0) 20 7583 5000
Здесь есть обзор всех наших офисов в Великобритании, включая местные
телефонные номера.
Контактная информация многих отдельных специалистов по обслуживанию и/или отрасли указана на соответствующих страницах. по всему сайту. Вы также можете отправить нам электронное письмо с вашими комментариями или предложениями
Если вы заинтересованы в работе в PwC, посетите раздел «Вакансии». сайт
La page que vous demandez est introuvable.
Essayez l’une des Solutions suivantes :
- Assurez-vous que l’adresse URL-адрес страницы, которая является правильной.
- Посетите страницу аккумулирования сайта.
- Посетите план сайта.
5.4 Масса и вес | University Physics Volume 1
Цели обучения
К концу раздела вы сможете:
- Объяснять разницу между массой и весом
- Объясните, почему падающие объекты на Земле никогда не находятся в состоянии свободного падения
- Опишите концепцию невесомости
Масса и вес часто используются как синонимы в повседневном разговоре. Например, наши медицинские записи часто показывают наш вес в килограммах, но никогда в правильных единицах измерения — ньютонах. Однако в физике есть важное различие. Вес — это притяжение Земли к объекту. Это зависит от удаленности от центра Земли. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны. 9{2}. [/latex]
Например, наши медицинские записи часто показывают наш вес в килограммах, но никогда в правильных единицах измерения — ньютонах. Однако в физике есть важное различие. Вес — это притяжение Земли к объекту. Это зависит от удаленности от центра Земли. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны. 9{2}. [/latex]
Хотя почти во всем мире в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее привычной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта. фунт человек весит 1000 Н.
Вес и гравитационная сила
Когда объект падает, он ускоряется по направлению к центру Земли. Второй закон Ньютона гласит, что результирующая сила, действующая на объект, отвечает за его ускорение. Если сопротивлением воздуха можно пренебречь, результирующая сила, действующая на падающий объект, представляет собой гравитационную силу, обычно называемую ее вес [латекс] \overset{\to }{w} [/латекс], или сила тяжести, действующая на объект массой м .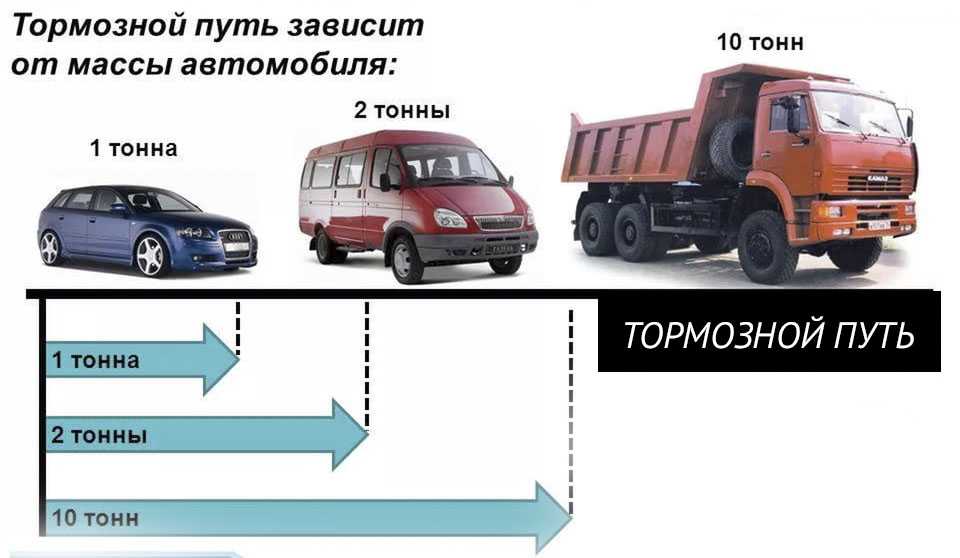 Вес можно обозначить как вектор, потому что он имеет направление; вниз — это, по определению, направление силы тяжести, и, следовательно, вес — это направленная вниз сила. Величина веса обозначается как w . Галилей сыграл важную роль в том, чтобы показать, что в отсутствие сопротивления воздуха все тела падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Вес можно обозначить как вектор, потому что он имеет направление; вниз — это, по определению, направление силы тяжести, и, следовательно, вес — это направленная вниз сила. Величина веса обозначается как w . Галилей сыграл важную роль в том, чтобы показать, что в отсутствие сопротивления воздуха все тела падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой м , падающий на Землю. На него действует только нисходящая сила тяжести, которая представляет собой вес [латекс] \overset{\to }{w} [/латекс]. Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна [латекс] {\ overset {\ to {F}} _ {\ text {net}} = m \ overset {\ to }{a}. [/latex] Мы знаем, что ускорение объекта под действием силы тяжести равно [латекс] \overset{\to }{g}, [/latex] или [латекс] \overset{\to }{a}=\overset{ \к {г} [/латекс]. Подставив их во второй закон Ньютона, мы получим следующие уравнения.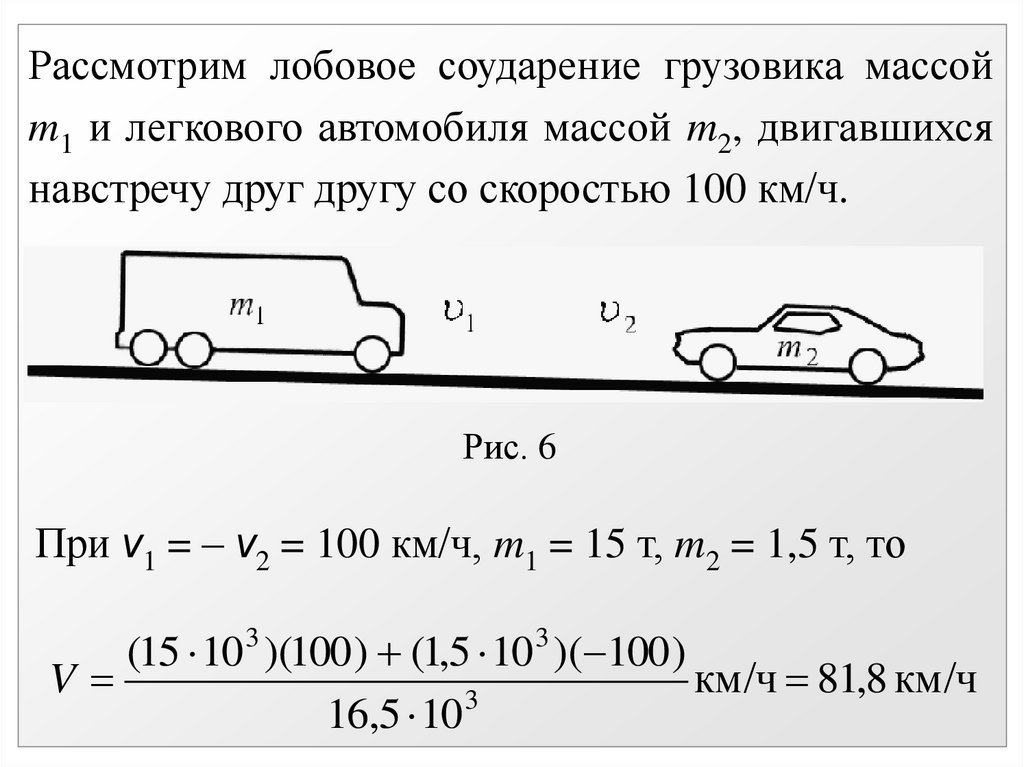 {2} [/латекс]. Таким образом, масса 1,0 кг имеет вес 90,8 с. ш. на Земле и всего около 1,7 с. ш. на Луне.
{2} [/латекс]. Таким образом, масса 1,0 кг имеет вес 90,8 с. ш. на Земле и всего около 1,7 с. ш. на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это гравитационная сила, действующая на него со стороны ближайшего крупного тела, такого как Земля, Луна или Солнце. Это наиболее распространенное и полезное определение веса в физике. Однако оно резко отличается от определения веса, используемого НАСА и популярными средствами массовой информации в связи с космическими путешествиями и исследованиями. Когда они говорят о «невесомости» и «микрогравитации», они имеют в виду явление, которое в физике называется «свободным падением». Мы используем предыдущее определение веса, силы [латекс] \overset{\to }{w} [/латекс] из-за гравитации, действующей на объект массой м , и мы тщательно различаем свободное падение и фактическую невесомость.
Имейте в виду, что вес и масса — разные физические величины, хотя и тесно связанные между собой. Масса — это внутреннее свойство объекта: это количество материи. Количество или количество материи объекта определяется количеством содержащихся в нем атомов и молекул различных типов. Поскольку эти числа не меняются, в ньютоновской физике масса не меняется; следовательно, его реакция на приложенную силу не меняется. Напротив, вес — это гравитационная сила, действующая на объект, поэтому он зависит от гравитации. Например, человек ближе к центру Земли, на небольшой высоте, такой как Новый Орлеан, весит немного больше, чем человек, который находится на большей высоте в Денвере, даже если они могут иметь одинаковую массу.
Количество или количество материи объекта определяется количеством содержащихся в нем атомов и молекул различных типов. Поскольку эти числа не меняются, в ньютоновской физике масса не меняется; следовательно, его реакция на приложенную силу не меняется. Напротив, вес — это гравитационная сила, действующая на объект, поэтому он зависит от гравитации. Например, человек ближе к центру Земли, на небольшой высоте, такой как Новый Орлеан, весит немного больше, чем человек, который находится на большей высоте в Денвере, даже если они могут иметь одинаковую массу.
Заманчиво приравнять массу к весу, потому что большинство наших примеров происходят на Земле, где вес объекта лишь немного зависит от местоположения объекта. Кроме того, трудно сосчитать и идентифицировать все атомы и молекулы в объекте, поэтому масса редко определяется таким образом. Если мы рассмотрим ситуации, в которых [латекс] \overset{\to }{g} [/latex] является константой на Земле, мы увидим, что вес [латекс] \overset{\to }{w} [/latex] непосредственно пропорциональна массе m , так как [латекс] \overset{\to }{w}=m\overset{\to }{g}, [/latex], то есть чем массивнее объект, тем больше он весит. {2} [/латекс], объект весит 8,4 Н. Однако масса объекта по-прежнему составляет 5,0 кг. на Луне. 9{2}? [/latex]
{2} [/латекс], объект весит 8,4 Н. Однако масса объекта по-прежнему составляет 5,0 кг. на Луне. 9{2}? [/latex]
Стратегия
Нам был дан вес камня, который мы используем для определения чистой силы, действующей на камень. Однако нам также необходимо знать его массу, чтобы применить второй закон Ньютона, поэтому мы должны применить уравнение для веса, [латекс] w = мг [/латекс], чтобы определить массу.
Решение
Никакие силы не действуют в горизонтальном направлении, поэтому мы можем сосредоточиться на вертикальных силах, как показано на следующей диаграмме свободного тела. Мы обозначаем ускорение в сторону; технически это не часть диаграммы свободного тела, но помогает напомнить нам, что объект ускоряется вверх (поэтому результирующая сила направлена вверх). 9{2})\hfill \\ \hfill F-180\,\text{N}& =\hfill & 27\,\text{N}\hfill \\ \hfill F& =\hfill & 207\,\text{ N}=210\,\text{N до двух значащих цифр}\hfill \end{array} [/latex]
Значение
Чтобы применить второй закон Ньютона в качестве основного уравнения при решении задачи, иногда приходится полагаться на другие уравнения, например, на вес или одно из кинематических уравнений, чтобы завершить решение.
Проверьте свои знания
Для (Пример) найдите ускорение, когда сила, приложенная фермером, равна 230,0 Н.
Показать раствор
Сможете ли вы избежать поля с валунами и благополучно приземлиться прямо перед тем, как закончится топливо, как это сделал Нил Армстронг в 1969 году? Эта версия классической видеоигры точно имитирует реальное движение лунного посадочного модуля с правильной массой, тягой, расходом топлива и лунной гравитацией. Настоящим лунным посадочным модулем трудно управлять.
Используйте эту интерактивную симуляцию, чтобы перемещать Солнце, Землю, Луну и космическую станцию, чтобы увидеть влияние их гравитационных сил и орбитальных траекторий. Визуализируйте размеры и расстояния между различными небесными телами и отключите гравитацию, чтобы увидеть, что было бы без нее. 9{2} [/латекс]. В этой задаче силы действуют на сиденье и ремень безопасности.
Тело массой 2,00 кг толкают вертикально вверх под действием вертикальной силы 25,0 Н.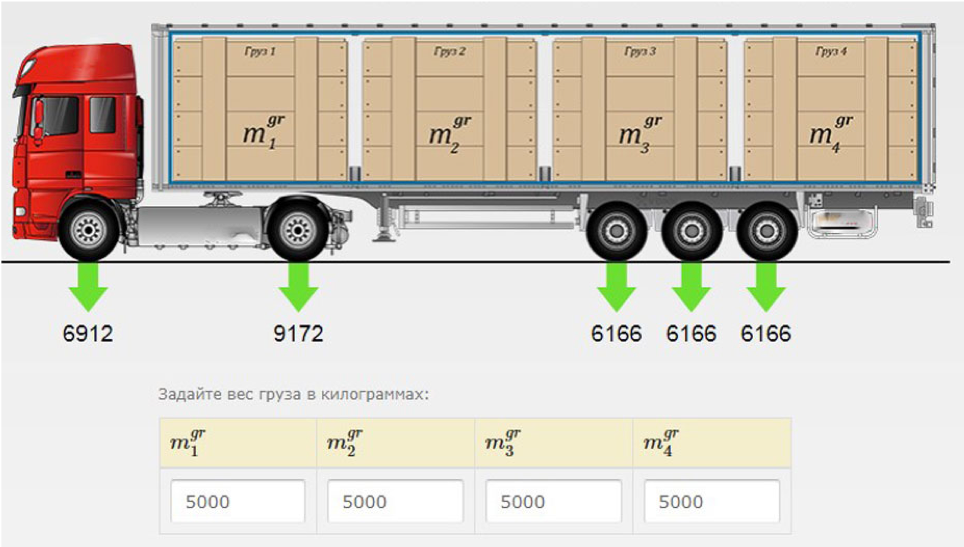
 Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера
Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера
 dk
dk