Июн
22
2023

Номер регионов: Коды регионов на автомобильных номерах России 2023 таблица и обозначения

Posted by

Регионы — Коды регионов России

Снимки экрана (iPhone)

Описание

Самый полный (обновленный!) справочник автомобильных кодов (индексов) регионов Российской Федерации.

• Быстрый поиск региона по коду
• Краткая информация о субъекте
• Местоположение на карте
• Самый полный! список кодов
• Поиск кода по названию региона или административного центра
• Обновление базы кодов онлайн
• Изменение иконки приложения на иконку со своим кодом региона, либо любого другого

———
Будем признательны за оценки и отзывы о приложение.
Спасибо! Пользуйтесь с удовольствием.

Версия 2.2.3

В версии приложения 2.2 вышел небольшой баг, связанный с дополнением базы кодов, добавилась новая информация о регионах и предыдущая версия базы никак не совмещается с новой, поэтому приложение вылетало при открытии.

В итоге, чтобы всё заработало необходимо удалить приложение и заново скачать. Сорри за неудобство, и в качестве извинений мы сделали изменение иконки приложения БЕСПЛАТНЫМ 😉 для всех иконок.

———
Версия 2.2.3
• Исправление ошибок

———
Версия 2.2.2
• Бесплатное изменение иконки приложения для всех иконок

———
Версия 2.2
• Темная тема (системная)
• Темные иконки приложения (2 шт.)
• Новая информация о регионах
— Население админ. центра
— Население региона
— Код ISO 3166-2

———
Будем признательны за оценки и отзывы о приложение.
Спасибо! Пользуйтесь с удовольствием.

Оценки и отзывы

Оценок: 528

Неплохо.

сенкс за приложение!

Коды новых регионов

База кодов без новых субъектов. Когда планируется обновление?

Приложение отличное

Вопрос: когда будет обновление базы кодов?

Обязательно! Спасибо за отзыв.

Разработчик Evgeny Konkin не сообщил Apple о своей политике конфиденциальности и используемых им способах обработки данных. Подробные сведения доступны в политике конфиденциальности разработчика.

Нет сведений

Разработчик будет обязан предоставить сведения о конфиденциальности при отправке следующего обновления приложения.

Информация

Провайдер
Evgeny Konkin

Размер
53 МБ

Категория
Справочники

Возраст
4+

Copyright
© Евгений Конкин

Цена
Бесплатно

  • Сайт разработчика
  • Поддержка приложения
  • Политика конфиденциальности

Вам может понравиться

коды регионов РФ | Учебный комбинат

Автошкола в Омске с обучением вождению по низким ценам

  1. Экзамены
  2. Полезная информация
  3. коды регионов РФ

Номера для автомобиля выдаются сразу же после его регистрации в ГИБДД и остаются на своем месте до тех пор, пока один из следующих владельцев не решит их заменить.

Регистрационные знаки являются уникальными, т.е. не может существовать одинаковых номеров у двух разных автомобилей. Номера всегда отличаются хотя бы на одну букву или цифру. Сегодня будут рассмотрены особенности и порядок выдачи автомобильных номеров, а также автомобильные коды регионов на номерах.

 

В Российской Федерации большинство регистрационных знаков имеют следующий вид:

Именно такие номера устанавливаются на большинство автомобилей.

На первый взгляд номер состоит из «каких-то» малопонятных букв и цифр. На самом деле не все здесь просто так.

На автомобильных номерах используются цифры от 0 до 9. Но в отличие от цифр, не все буквы русского алфавита могут оказаться на номерах. Такая привилегия дана только тем буквам, которые имеют схожие по написанию символы в латинском алфавите. Т.е. на автономерах могут использоваться только буквы А, В, Е, К, М, Н, О, Р, С, Т, У, Х.

Об этом факте Вы могли узнать и раньше, но вот следующая мысль наверняка покажется Вам интересной.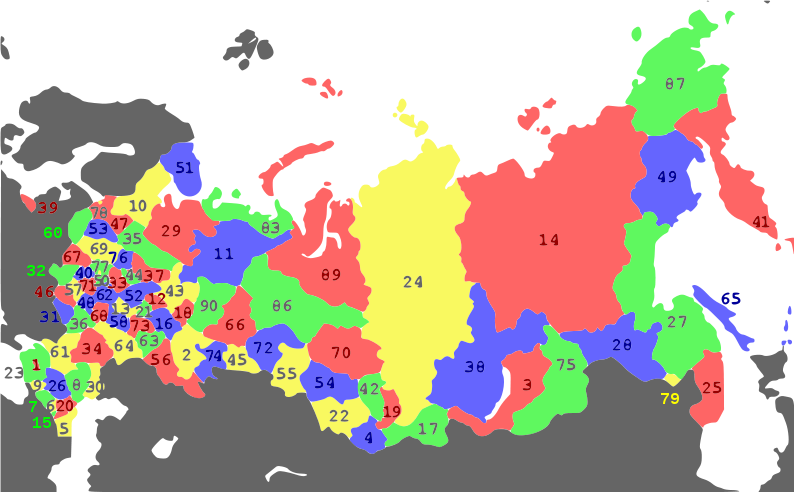 Речь пойдет о том, каков порядок выдачи номеров.

Номера выдаются по порядку (кроме специальных серий). Однако порядок изменения символов в номере далек от нормального восприятия. Символы меняются не справа налево, а несколько по другому — в достаточно запутанной последовательности.

1. Чаще всего в автомобильном номере меняется 3я цифра (на рисунке это цифра 6). После номера Т356ОК будет выдан номер Т357ОК.

2. Второй по частоте изменения символ — 2я цифра (на рисунке 5). После номера Т359ОК будет выдан номер Т360ОК.

3. Третий по частоте символ — 1я цифра (на рисунке 3). После номера Т399ОК будет выдан номер Т400ОК.

С цифрами вроде бы все в порядке, но того же самого нельзя сказать о буквах.

4. Четвертый по частоте символ — 1я буква (на рисунке Т). После номера Т999ОК будет выдан номер У001ОК.

5. Пятый по частоте символ — 3я буква (на рисунке К). После номера Х999ОК будет выдан номер А001ОМ.

6. Шестой по частоте символ — 2я буква (на рисунке О). После номера Х999ОХ будет выдан номер А001РА.

Порядок достаточно сложен, так что если не поняли его с первого раза, перечитайте пункты 1-6 еще раз.

До сих пор речь в статье шла о шести левых символах регистрационного знака. Они отвечают за номера автомобилей внутри конкретного региона. Кстати, любителям статистики сообщаю, что в одном регионе может быть выдано не более чем 1 млн 726 тыс 272 автомобильных регистрационных знаков.

После исчерпания такого лимита происходит изменение номера региона России, записанного в правой части номера. После этого номера начинают выдаваться заново внутри нового региона. Каждому субъекту российской федерации соответствует собственный код, а некоторым субъектам федерации, имеющим очень большое число автомобилей, присвоены одновременно несколько кодов региона.

 

 

 

КодСубъект Российской Федерации
01Республика Адыгея
02, 102Республика Башкортостан
03Республика Бурятия
04Республика Алтай (Горный Алтай)
05Республика Дагестан
06Республика Ингушетия
07Кабардино-Балкарская Республика
08Республика Калмыкия
09Республика Карачаево-Черкессия
10Республика Карелия
11Республика Коми
12Республика Марий Эл
13, 113Республика Мордовия
14Республика Саха (Якутия)
15Республика Северная Осетия — Алания
16, 116Республика Татарстан
17Республика Тыва
18Удмуртская Республика
19Республика Хакасия
21, 121Чувашская Республика
22Алтайский край
23, 93, 123Краснодарский край
24, 84, 88, 124Красноярский край
25, 125Приморский край
26Ставропольский край
27Хабаровский край
28Амурская область
29Архангельская область
30Астраханская область
31Белгородская область
32Брянская область
33Владимирская область
34, 134Волгоградская область
35Вологодская область
36Воронежская область
37Ивановская область
38, 85Иркутская область
39, 91Калининградская область
40Калужская область
41Камчатский край
42Кемеровская область
43Кировская область
44Костромская область
45 Курганская область
46Курская область
47Ленинградская область
48Липецкая область
49Магаданская область
50, 90, 150, 190Московская область
51Мурманская область
52, 152Нижегородская область
53Новгородская область
54Новосибирская область
55Омская область
56Оренбургская область
57Орловская область
58Пензенская область
59, 81, 159Пермский край
60Псковская область
61, 161Ростовская область
62Рязанская область
63, 163Самарская область
64, 164Саратовская область
65Сахалинская область
66, 96Свердловская область
67Смоленская область
68Тамбовская область
69Тверская область
70Томская область
71Тульская область
72Тюменская область
73, 173Ульяновская область
74, 174Челябинская область
75, 80Забайкальский край
76Ярославская область
77, 97, 99, 177, 197, 199, 777г. Москва
78, 98, 178г. Санкт-Петербург
79Еврейская автономная область
82Республика Крым
83Ненецкий автономный округ
86, 186Ханты-Мансийский автономный округ — Югра
87Чукотский автономный округ
89Ямало-Ненецкий автономный округ
92г. Севастополь
94Территории, находящиеся за пределами РФ и обслуживаемые Департаментом режимных объектов МВД России
95Чеченская республика

6.2: Топология — сколько регионов

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    58577
    • Санджой Махаджан
    • Инженерный колледж Олин через MIT OpenCourseWare

    Валентный угол в метане (раздел 6. 1) можно вычислить непосредственно с помощью аналитической геометрии (задача 6.3), так что рассуждения по аналогии не показывают всей своей силы. Поэтому попробуйте решить следующую задачу.

    Вопрос

    На сколько областей делят пространство пять плоскостей?

    Эта формулировка допускает вырожденные схемы, такие как пять параллельных плоскостей, четыре плоскости, сходящиеся в одной точке, или три плоскости, сходящиеся на одной линии. Чтобы устранить эти и другие вырождения, будем размещать и ориентировать плоскости случайным образом, тем самым максимально увеличивая количество областей. Затем задача состоит в том, чтобы найти максимальное количество областей, образованных пятью плоскостями.

    Трудно представить пять плоскостей, но метод простых случаев с использованием меньшего количества плоскостей может привести к модели, которая обобщается до пяти плоскостей. Самый простой случай — нулевые плоскости: пространство остается целым, поэтому \(R(0) = 1\) (где R(n) обозначает количество областей, созданных n плоскостями).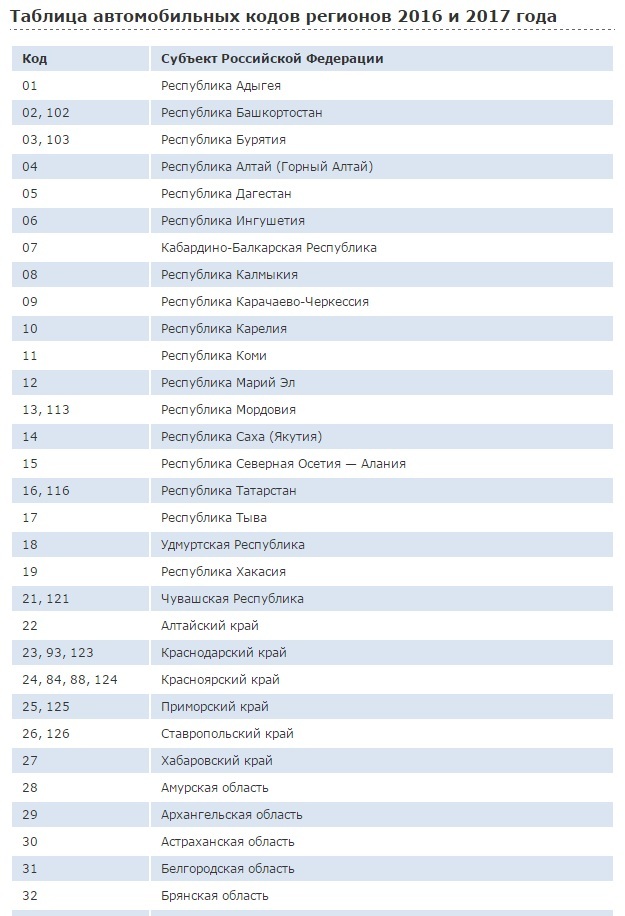 Первая плоскость делит пространство на две половины, что дает \(R(1) = 2\). Чтобы добавить вторую плоскость, представьте, что вы дважды разрезаете апельсин, чтобы получить четыре дольки: \(R(2) = 4\).

    Вопрос

    Какие шаблоны появляются в данных? 9{н}\). Чтобы проверить это, попробуйте случай \(n = 3\), разрезав апельсин в третий раз и разрезав каждую из четырех частей на две меньшие части; таким образом, \(R(3)\) действительно равно 8. Возможно, шаблон продолжается с \(R(4) = 16\) и \(R(5) = 32\). В следующей таблице для \(R(n)\) эти две экстраполяции отмечены серым цветом, чтобы отличить их от проверенных записей.

    9{n}\) гипотеза будет проверена дальше?

    Прямая проверка путем подсчета областей затруднена, поскольку эти области трудно визуализировать в трех измерениях. Аналогичную двумерную задачу было бы решить легче, и ее решение может помочь проверить гипотезу о трехмерности. Двумерное пространство разделено линиями, поэтому аналогичный вопрос следующий:

    Вопрос

    Каково максимальное количество областей, на которые n прямых делят плоскость? 9{n}\) гипотеза, вероятно, применима к трем измерениям.

    Вопрос

    Что происходит в нескольких простых случаях?

    Нулевые линии покидают плоскость целиком, что дает \(R(0) = 1\). Следующие три случая таковы (хотя см. задачу 6.5):

    Множественные задачи

    Задача 6.5 Снова три линии

    На рисунке \(R(3) = 7\) показаны три линии, дающие семь областей. Вот еще один пример с тремя линиями, также расположенными в случайном порядке, но, похоже, получается только шесть областей. Где и где находится седьмой регион? Или \(R(3) = 6\)? 9{n}\) гипотеза мертва.

    Если рассматривать двумерные данные \(R_{2}(n)\) вместе с трехмерными данными \(R_{3}(n)\), может возникнуть новая гипотеза.

    нет 0 1 2
    нет 0 1 2 3 4
    \(R_{2}\) 1 2 4 7 11
    \(R_{3}\) 1 2 4 8

    В этой таблице несколько записей объединяются в соседние записи. Например, \(R_{2}(1)\) и \(R_{3}(1)\) две записи в столбце \(n = 1\) суммируются в \(R_{2}(2) \) или \(R_{3}(2)\). Эти две записи, в свою очередь, суммируются в запись \(R_{3}(3)\). Но в таблице есть много маленьких чисел с множеством способов их комбинирования; отбрасывание совпадений требует сбора дополнительных данных, и простейшим источником данных является аналогичная одномерная задача.

    Вопрос

    На какое максимальное количество отрезков n точек делят прямую?

    Заманчивый ответ: n точек составляют n отрезков. Однако простой случай, когда одна точка дает два сегмента, уменьшает искушение. Скорее, \(n\) точек составляют \(n + 1\) сегментов. Этот результат генерирует строку \(R_{1}\) в следующей таблице.

    нет 0 1 2 3 4 5 п
    \(R_{1}\) 1 2 3 4 5 6 п + 1
    \(R_{2}\) 1 2 4 7 11
    \(R_{3}\) 1 2 4 8

    Вопрос

    Какие закономерности присутствуют в этих данных?

    Гипотеза 2n выживает частично. В строке \(R_{1}\) происходит сбой, начиная с \(n = 2\). В строке \(R_{2}\) происходит сбой, начиная с \(n = 3\). Таким образом, в строке \(R_{3}\) он, вероятно, терпит неудачу, начиная с \(n = 4\), делая предположения\(R_{3}\)(4) = 16 и \(R_{3}( 5) = 32\) маловероятно. Моя личная оценка состоит в том, что до появления этих неудач вероятность гипотезы \(R_{3}(4) = 16\) составляла 0,5; но теперь он падает не более чем до 0,01. (Подробнее об оценке и обновлении вероятностей гипотез см. важные работы по правдоподобным рассуждениям Корфилда [11], Джейнса [21] и Полиа [36].)

    В лучших новостях очевидные совпадения содержат надежную закономерность:

    Вопрос

    Если схема продолжается, на сколько областей пять плоскостей могут разделить пространство?

    По выкройке,

    \[R_{3}(4) = \underbrace{R_{2}(3)}_{7} + \underbrace{R_{3}(3)}_{8} = 15 \label{6.2} \ ]

    , а затем

    \[R_{3}(5) = \underbrace{R_{2}(4)}_{11} + \underbrace{R_{3}(4)}_{15} = 26. \label{6.3} \]

    Таким образом, пять плоскостей могут разделить пространство максимум на 26 областей.

    Это число трудно вывести, рисуя пять плоскостей и считая области. Кроме того, такой подход грубой силы даст значение только \(R_{3}\)(5), тогда как простые случаи и аналогия дают метод для вычисления любой записи в таблице. Таким образом, они предоставляют достаточно данных, чтобы предположить выражения для \(R_{2}\)(n) (задача 6.9), для \(R_{3}\)(n) (задача 6.10) и для общего элемента \(R_ {d}\)(n) (задача 6.12).

    Множественные проблемы

    Задача 6.7 Проверка шаблона в двух измерениях

    Предполагаемый шаблон предсказывает \(R_{2}(5) = 16\): пять линий могут разделить плоскость на 16 областей. Проверьте гипотезу, нарисовав пять линий и посчитав области.

    Задача 6.8 Бесплатные данные из нулевых измерений

    Поскольку одномерная задача дала полезные данные, попробуйте решить нульмерную задачу. Расширьте шаблон для строк \(R_{3}\), \(R_{2}\) и \(R_{1}\) вверх, чтобы построить строку \(R_{0}\). Он дает количество нульмерных областей (точек), полученных путем разделения точки на n объектов (размерность -1). Что такое \(R_{0}\), если строка должна следовать наблюдаемому образцу? Согласуется ли этот результат с геометрическим смыслом попытки разделить точку? 9{2}\), для \(n = 0…2\). Если остаток не является линейным по n, то остается квадратичный член или было удалено слишком много. В любом случае отрегулируйте A.

    b. Как только квадратичный коэффициент A окажется правильным, используйте аналогичную процедуру, чтобы найти линейный коэффициент B.

    c. Аналогично решить постоянный коэффициент C.

    d. Проверьте свою квадратичную подгонку по новым данным (\(R_{2}(n)\) для \(n \geqslant 3\)).

    Задача 6.10 Общий результат в трех измерениях

    Разумно предположить, что строка \(R_{3}\) соответствует кубической (задача 6.9). Используйте удаление большой части, чтобы подогнать куб к данным \(n = 0 . . . 3\). Выдает ли он предполагаемые значения \(R_{3}(4) = 15\) и \(R_{3}(5) = 26\)?

    Задача 6. 11 Геометрическое объяснение

    Найдите геометрическое объяснение наблюдаемой закономерности. Подсказка: Сначала объясните, почему шаблон генерирует строку \(R_{2}\) из строки \(R_{1}\); затем обобщите причину, чтобы объяснить строку \(R_{3}\).

    Задача 6.12 Общее решение в произвольной размерности

    Образ, соединяющий соседние записи таблицы \(R_{d}(n)\), есть образ, порождающий треугольник Паскаля [17]. Поскольку треугольник Паскаля дает биномиальные коэффициенты, общее выражение \(R_{d}(n)\) должно содержать биномиальные коэффициенты.

    Поэтому используйте биномиальные коэффициенты, чтобы выразить \(R_{0}(n)\) (задача 6.8), \(R_{1}\)(n) и \(R_{2}\)(n) ( Задача 6.9). Затем предположите форму биномиального коэффициента для \(R_{3}\)(n) и \(R_{d}\)(n), сверив результат с задачей 6.10. 9{n}\) для \(n \leqslant d\) (возможно, используя результаты задачи 6.12).

    Эта страница под названием 6. 2: Топология — сколько регионов используется совместно по лицензии CC BY-NC-SA 4.0, автором, ремиксом и/или куратором которой является Санджой Махаджан (MIT OpenCourseWare) с использованием исходного содержимого, отредактированного в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Санджой Махаджан
        Лицензия
        CC BY-NC-SA
        Версия лицензии
        4,0
        Программа OER или Publisher
        MIT OpenCourseWare
        Показать страницу TOC
        нет
      2. Теги
        1. source@https://ocw.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *